|
1. Getriebenes gedämpftes Pendel
Auch das sinusförmig angetriebene, gedämpfte Pendel ist ebenso wie das Lorenz-System ein System mit kontinuierlicher Zeitskala und drei Freiheitsgraden. Seine Bewegung beschreibt folgendes Differentialgleichungssystem:
Darin bedeuten x den Winkel der Auslenkung, v die Winkelgeschwindigkeit,  die Dämpfung, a die
Antriebsamplitude, die Dämpfung, a die
Antriebsamplitude, 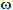 die (Kreis-)Frequenz des Antriebs und die (Kreis-)Frequenz des Antriebs und 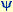 die Phase des Antriebs. Die Pendelmasse ist dabei durch eine feste Stange, nicht durch einen Faden mit der Drehachse verbunden, so daß Auslenkungen über die
Horizontalstellung hinaus und sogar Überschläge möglich sind. die Phase des Antriebs. Die Pendelmasse ist dabei durch eine feste Stange, nicht durch einen Faden mit der Drehachse verbunden, so daß Auslenkungen über die
Horizontalstellung hinaus und sogar Überschläge möglich sind.
Im Gegensatz zum Lorenzsystem gibt es hier einen Freiheitsgrad, die Antriebsphase 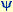 , der von den anderen
Freiheitsgraden unabhängig ist (3. Zeile des Differentialgleichungssystems), denn der Antrieb erfolgt gleichmäßig durch ein von außen auf die Pendelachse aufgeprägtes sinusförmiges Drehmoment und ist unabhängig von
momentanem Winkel und Winkelgeschwindigkeit. Ein solches System heißt nicht-autonom. , der von den anderen
Freiheitsgraden unabhängig ist (3. Zeile des Differentialgleichungssystems), denn der Antrieb erfolgt gleichmäßig durch ein von außen auf die Pendelachse aufgeprägtes sinusförmiges Drehmoment und ist unabhängig von
momentanem Winkel und Winkelgeschwindigkeit. Ein solches System heißt nicht-autonom.
Ein weiterer Unterschied zum Lorenzsystem liegt in der Periodizität des Phasenraums. Es genügt, Antriebsphase 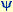 und Winkel x
jeweils auf das Intervall [- und Winkel x
jeweils auf das Intervall [- ... ...  ] zu beschränken, da es zur Festlegung des Pendelzustands unerheblich ist, wieviel Antriebsperioden bereits vergangen sind und ob und wie oft sich das Pendel überschlagen hat. ] zu beschränken, da es zur Festlegung des Pendelzustands unerheblich ist, wieviel Antriebsperioden bereits vergangen sind und ob und wie oft sich das Pendel überschlagen hat.
Abhängig von der Stärke und Periode des Antriebs kann das Pendel ganz unterschiedliche Attraktoren ausbilden. Bei
verschwindendem Antrieb ist die Ruhelage stabiler Fixpunkt der Bewegung (in diesem Grenzfall reduziert sich der Phasenraum auf 2 Freiheitsgrade, da der Antrieb wegfällt). Bei kleiner Antriebsperiode folgt das Pendel mit einer
gewissen Phasenverschiebung dem antreibenden Moment, der Attraktor ist dann ein stabiler periodischer Orbit, gegen den jede Trajektorie des Pendels nach einem Einschwingvorgang konvergiert. Bei geeigneter Wahl der
Antriebsparameter kann das Pendel aber auch ganz irreguläre Bewegungen vollführen, sich überschlagen und scheinbar regellos bewegen. In dieser chaotischen Phase folgt die Trajektorie einem seltsamen Attraktor.
Das Pendel startet aus der Ruhelage mit voreingestellter Antriebsfrequenz und Amplitude, die Bewegung folgt dann dem unten dargestellten seltsamen Attraktor. Links ist das Pendel selbst, rechts seine Trajektorie im Phasenraum
dargestellt mit den Achsen x (rot), v (grün) und psi (blau). Die Trajektorienstücke sind entlang der psi-Achse mit einem Farbverlauf von blau nach rot dargestellt, um
den räumlichen Eindruck zu unterstützen. Mit der Maus läßt sich dieser Phasenraumwürfel frei drehen. Über die Listbox lassen sich neben dem Attraktor auch die instabilen periodischen Orbits mit der Länge einer Antriebsperiode auswählen. Die Pendelbewegung folgt dann dem jeweiligen Orbit. Wenn
der Knopf "manual" gedrückt wird, lassen sich Antriebsperiode und -frequenz mit den Schiebereglern verändern.
Ein solches angetriebenes Pendel wurde am Physikalischen Institut der Uni Frankfurt experimentell realisiert [Heng92] und dient dort seit über 10 Jahren als Demonstrationsobjekt [Heng94], [Hübinger94], [Doerner94]. Unter
anderem wurden an diesem Aufbau Untersuchungen zur Vorhersagbarkeit [Doerner93], [Doerner94b], [Doerner99], [Doerner99b] durchgeführt und Methoden zur Steuerung chaotischer Bewegungen getestet [Hübinger93], [Hübinger94a], [Doerner95]
Der seltsame Attraktor des Pendels bei den Systemparametern 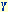 = 0.052, a = 0.586, = 0.052, a = 0.586,  = 0.666. Der Blick ist schräg auf den Phasenraum gerichtet Die roten "Schnittflächen" sind Poincaré-Schnitte durch den Phasenraum bei = 0.666. Der Blick ist schräg auf den Phasenraum gerichtet Die roten "Schnittflächen" sind Poincaré-Schnitte durch den Phasenraum bei 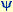 = 0 (Schnittfläche vorne rechts), bzw. bei x = - = 0 (Schnittfläche vorne rechts), bzw. bei x = - (Schnittfläche vorne links). Vertikal ist die Winkelgeschwindigkeit aufgetragen, blau ist die Einhüllende des
Attraktors. Man erkennt wie schon beim Hénon-Attraktor gut die "blätterteigartige" fraktale Struktur und die Periodizität in den Koordinaten Winkel und Antriebsphase. (Schnittfläche vorne links). Vertikal ist die Winkelgeschwindigkeit aufgetragen, blau ist die Einhüllende des
Attraktors. Man erkennt wie schon beim Hénon-Attraktor gut die "blätterteigartige" fraktale Struktur und die Periodizität in den Koordinaten Winkel und Antriebsphase.
     
Der Schnitt des Pendel-Attraktors (bei den gleichen Systemparametern) mit einer Poincaré-Ebene 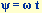 , deren Phase mit der Zeit
immer weiterläuft, so daß sich der Eindruck eines Filmes ergibt. Der Poincaré-Schnitt ist mehrmals nebeneinander gedruckt, so daß die Periodizität im Auslenkungswinkel schön sichtbar wird. , deren Phase mit der Zeit
immer weiterläuft, so daß sich der Eindruck eines Filmes ergibt. Der Poincaré-Schnitt ist mehrmals nebeneinander gedruckt, so daß die Periodizität im Auslenkungswinkel schön sichtbar wird.
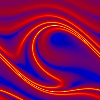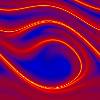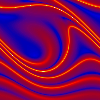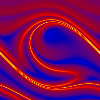     
Der effektive Lyapunov-Exponent ist ein Maß für die Vorhersagbarkeit der Pendelbewegung in der nächsten Zukunft. Hier ist er für eine Vorhersagezeit von 1 Antriebsperiode auf einer Poincaré-Ebene 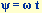 . dargestellt, deren Phase mit der Zeit immer weiterläuft,
so daß sich der Eindruck eines Filmes ergibt. Der Poincaré-Schnitt ist auch hier wieder mehrmals nebeneinander gedruckt, um die Periodizität im Auslenkungswinkel hervorzuheben. . dargestellt, deren Phase mit der Zeit immer weiterläuft,
so daß sich der Eindruck eines Filmes ergibt. Der Poincaré-Schnitt ist auch hier wieder mehrmals nebeneinander gedruckt, um die Periodizität im Auslenkungswinkel hervorzuheben.
2. Doppelpendel (ohne Antrieb und ohne Dämpfung)
Dieses konservative System besteht aus einem größeren Pendel und einem kleinerem Pendel, dessen Drehachse mit
dem Ende des größeren verbunden ist. Beide Pendel schwingen in der gleichen Ebene, Überschläge sind möglich. Der idealisierte Fall eines ungedämpften Pendels wird durch das folgende Gleichungssystem beschrieben:
|
dx/dt =
|
y
|
|
dy/dt =
|
[-cv2sin(x-u) - y2sin(x-u)cos(x-u) + b sin(u)cos(x-u) - abc sin(x)] / [ac - cos2(x-u)]
|
|
du/dt =
|
v
|
|
dv/dt =
|
[ ay2sin(x-u) + v2sin(x-u)cos(x-u) + ab sin(x)cos(x-u) - ab sin(u)] / [ac - cos2(x-u)]
|
|
Darin bedeuten x und y den Auslenkungswinkel und die Winkelgeschwindigkeit des größeren Pendels, u und v die des kleineren Pendels. a, b und c
sind Konstanten, die die Längen- und Massenverhältnisse der beiden Pendel beschreiben. Das ungestörte System bewegt sich in seinem 4-dimensionalen Phasenraum auf einer 3-dimensionalen
Hyperfläche konstanter Energie. Anders gesagt: wenn man die (konstante) Gesamtenergie des Systems kennt, reichen 3 Variablen aus, um den Systemzustand eindeutig festzulegen.
Das Doppelpendel startet aus einer definierten Anfangsposition. Links ist das Pendel selbst dargestellt, es kann mit der Maus in eine neue Ausgangsposition gebracht werden.
Die rechte Seite zeigt eine 3-dimensionale Projektion seines 4-dimensionalen Phasenraums. Dieser Würfel ist mit gedrückter linker Maustaste drehbar und wird von den Variblen x, y und u aufgespannt.
Appendix: Vom physischen getriebenen Pendel zur dimensionslosen Pendelgleichung
Die physikalischen Größen, die ein angetriebenes Pendel charakterisieren, sind sein Massenträgheitsmoment I (mit der Maßeinheit kg m2), seine Dämpfung 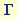 (mit der Maßeinheit kg m2s-1), das Rückstellmoment M, das es bei
Auslenkung um den Winkel 90° erfährt (mit der Maßeinheit N m = kg m2s-2) und das sinusförmig antreibende Drehmoment mit der Amplitude A (ebenfalls mit der Maßeinheit N m = kg m2s-2
) und der Kreisfrequenz (mit der Maßeinheit kg m2s-1), das Rückstellmoment M, das es bei
Auslenkung um den Winkel 90° erfährt (mit der Maßeinheit N m = kg m2s-2) und das sinusförmig antreibende Drehmoment mit der Amplitude A (ebenfalls mit der Maßeinheit N m = kg m2s-2
) und der Kreisfrequenz 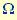 (mit der Maßeinheit s-1
). Mit diesen Größen lautet die Bewegungsgleichung: (mit der Maßeinheit s-1
). Mit diesen Größen lautet die Bewegungsgleichung:
Darin bedeuten x den Auslenkungswinkel und 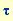 die Zeit. Diese Gleichung läßt sich in eine dimensionslose Form
bringen, indem man sie durch M teilt und die Zeit die Zeit. Diese Gleichung läßt sich in eine dimensionslose Form
bringen, indem man sie durch M teilt und die Zeit 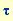 durch die dimensionslose Zeit durch die dimensionslose Zeit  substituiert. Der
letzte Schritt bedeutet anschaulich eine Normierung der Zeit auf die Schwingungsdauer, die das Pendel ohne Antrieb (A=0) bei kleiner Amplitude hat. Man erhält so:
Mit der Einführung neuer Koeffizienten substituiert. Der
letzte Schritt bedeutet anschaulich eine Normierung der Zeit auf die Schwingungsdauer, die das Pendel ohne Antrieb (A=0) bei kleiner Amplitude hat. Man erhält so:
Mit der Einführung neuer Koeffizienten 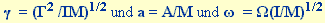 erhält man daraus die
oben dargestellte dimensionslose Differentialgleichung des Pendels. erhält man daraus die
oben dargestellte dimensionslose Differentialgleichung des Pendels.
|



